Matematicas

Ecuación de segundo grado

Una ecuación de segundo grado o ecuación cuadrática es una ecuación algebraica de segundo grado.^1 2 Es decir que la mayor potencia de la incógnitaconsiderada en la ecuación, es dos. La expresión general de una ecuación cuadrática es

donde x representa la variable y a, b y c son constantes; a es un coeficientecuadrático (distinto de 0), b el coeficiente lineal y c es el término independiente.

La gráfica de una función cuadrática es una parábola. La ecuación cuadrática proporciona las intersecciones de la parábola con el eje de las abscisas, que pueden ser en dos puntos, en uno o ninguno.

Fórmula cuadrática

De una ecuación cuadrática con coeficientes reales o complejos existen siempre dos soluciones, no necesariamente distintas, llamadas raíces, que pueden ser reales o complejas. Se denomina fórmula cuadrática³ a la ecuación que proporciona las raíces de la ecuación cuadrática:

 ,

donde el símbolo ± indica que los valores

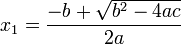
y

constituyen las dos soluciones.

DISCRIMINANTE 

En la fórmula anterior, la expresión dentro de la raíz cuadrada recibe el nombre dediscriminante de la ecuación cuadrática. Suele representarse con la letra D o bien con el símbolo Δ (delta):

Una ecuación cuadrática con coeficientes reales tiene o bien dos soluciones reales distintas o una sola solución real de multiplicidad 2, o bien dos raíces complejas. El discriminante determina la índole y la cantidad de raíces.

• Dos soluciones reales y diferentes si el discriminante es positivo (la parábola cruza dos veces el eje de las abscisas: X):

.

• Una solución real doble si el discriminante es cero (la parábola sólo toca en un punto al eje de las abscisas: X):

• Dos números complejos conjugados si el discriminante es negativo (la parábola no corta al eje de las abscisas: X):

donde i es la unidad imaginaria.

En conclusión, las raíces son distintas si el discriminante es no nulo, y son números reales si –sólo si– el discriminante es no negativo.